Законы логического вывода
Умение делать выводы - основная способность любого интеллекта. Основным признаком интеллекта являются знания и умения решать определенные задачи. Основой этих интеллектуальных умений являются законы и принципы логического вывода.
Законы человеческого мышления изучаются логикой и психологией. Принципы искусственного интеллекта разрабатываются в математической логике и информатике на основе методов машинного доказательства теорем и постановки экспериментов на ЭВМ.
Знание законов логического вывода позволяет выверять правильность рассуждений, доказательств, а также находить ошибочные утверждения. Незнание или нарушение этих законов и принципов приводит к логическим ошибкам и принятию неправильных решений.
В качестве иллюстраций рассмотрим базу знаний о семье. Пусть в семье есть дочь Оля, сын Сережа, мама Надя, папа Коля, бабушка Зина и дедушка Миша:
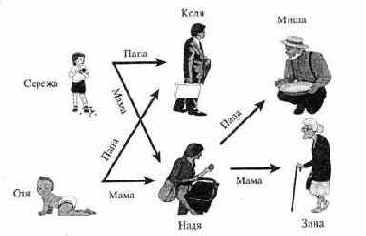
Соответствующая база данных на языке Пролог:
мама (Зина, Надя); папа (Миша, Надя);
мама (Надя, Оля); папа (Коля, Оля);
мама (Надя, Сережа); папа (Коля, Сережа);
Система Пролог при наличии этих фактов в памяти ЭВМ даст следующие ответы на вопросы о «папах» и «мамах»:
? мама (Надя, Оля) - Надя - мама Оли?
да
? папа (Сережа, Надя) - Сережа - папа Нади?
нет
Машина, использующая систему Пролог, дает ответы строго в соответствии с определенными логическими законами и принципами логического вывода. Разберем эти законы и принципы.
Законы логики - это общие законы логического вывода, используемые для вывода различных умозаключений. Наличие интеллекта и у компьютеров и у людей определяется прежде всего способностями делать выводы и умозаключения в различных ситуациях.
Закон противоречия - первый общий закон логики. Этот закон впервые высказал Аристотель - основатель логики как научной дисциплины:
А и не А - Не могут быть истинны одновременно
ложь суждение и его отрицание
Примеры противоречивых утверждений:
1) «яблоко - спелое»;
«яблоко - неспелое»;
2) «треугольник АВС - прямоугольный»;
«стороны треугольника равны друг другу».
Высказывание противоречивых суждений и утверждений является примером серьезных логических ошибок. Наличие противоречий говорит о некотором умысле либо о нарушениях в сознании.
В системе Пролог закон противоречия лежит в основе механизмов вывода ответов на вопросы. А именно, система Пролог для каждого вопроса формирует его отрицание и для этого отрицания ищет противоречие по отношению к фактам и правилам в базе знаний, хранящейся в памяти.
Так, вопрос ? мама (Надя, Оля) ЭВМ преобразует в отрицание не мама (Надя, Оля)
и временно присоединяет его к базе знаний. При этом получившаяся база становится противоречивой и система Пролог объявляет отрицание ложным и выводит ответ ДА.
Закон исключения третьего - второй общий закон логики, указанный Аристотелем:
А или не А - Истинно суждение либо его отрицание,
истина третьего не дано.
Примеры взаимоисключающих утверждений:
1) «Сегодня будет дождь» или «Сегодня дождя не будет».
2) «Любой треугольник правильный либо в нем есть разные стороны».
Принципы логического вывода в системе Пролог отличаются от законов Аристотеля, поскольку его законы выражаются на языке высказываний, а работа системы Пролог основана на использовании предикатов.
Соответствующая запись законов логики на языке исчисления предикатов представляет конструктивные процедуры, позволяющие осуществлять конкретные логические выводы из общих правил и конкретных фактов.
Закон противоречия в записи на языке исчисления предикатов преобразуется в процедуру вывода ответов на простейшие вопросы вида ? А(с):
А(х) и не А(с) - При противоречии А(х) и не А(с)
ложь, при х = с контрпримером служит х = с.
Содержательный смысл: При противоречии А(х) и не А(с) контрпримером служит х = с. Здесь х - переменная, а с
- конкретное значение, при котором отрицание ответа оказывается ложным. Это значение х = с выводится системой Пролог в качестве ответа на поставленный вопрос. Примеры такого рода вопросов и ответов:
? папа (х, Коля) - Кто папа у Коли ?
нет
? папа (х, Оля) - Кто папа у Оли ?
х = Коля
? мама (х, у) - Что известно о мамах?
х = Зина у = Надя
х = Надя у = Оля
Закон двойного отрицания - третий общий закон логики. Этот закон также был высказан Аристотелем:
не (не А) - Если неверно отрицание,
А то суждение – истинно
Примеры рассуждений.
1) Неверно, что «Вчера не было дождя».
Следовательно, «Вчера был дождь».
2) Неправда, что «это сделал не Саша».
Следовательно, «это сделал Саша». (?)
Из второго примера видно, что закон двойного отрицания является косвенным доказательством, поскольку оно не опирается на факты или аргументы. По этим причинам закон двойного отрицания может оказаться ошибочным и этот закон не является общезначимым (верным для всех случаев и ситуаций).
Правильность утверждений и рассуждений даже при безупречной логике доказательств зависит от достоверности исходных фактов и положений. Эту идею выражает четвертый общий логический закон - закон достаточных оснований, впервые сформулированный Лейбницем - создателем одной из самых первых механических вычислительных машин и основателем исчисления предикатов.
Закон достаточных оснований:
Всякое утверждение должно предполагать существование аргументов и фактов, достаточных для его обоснования.
Иными словами, любое утверждение должно предполагать наличие набора конкретных фактов и правил, из которых должно вытекать утверждаемое. Нарушениями это закона являются рассуждения, опирающиеся на недостоверные факты или положения, истинность которых не проверяется, а принимается на веру.
Пример рассуждений, не имеющих достаточных оснований:
1. «Если дорогу перебежала черная кошка, то быть неприятностям».
2. «Это верно, потому что это - справедливо».
Экспертные системы на ЭВМ с этой точки зрения должны создаваться исключительно на основе достоверных данных и общих правил вывода, проверенных практикой. Включение в базу знаний недостоверных данных или неподтвержденных обобщений и правил может привести к появлению ошибок и получению неправильных решений.
Причина такой работы экспертных систем состоит в том, что компьютеры могут делать выводы и
умозаключения только исходя из фактов и правил, имеющихся в базе знаний, и только из этих данных - и ничего другого. Практическую ценность для систем машинного интеллекта представляют принципы логического вывода на основе не только фактов, но и правил.
Закон логического вывода
modus ponens - первый закон, указанный Аристотелем:
А ® В, А -
Если из А следует В и посылка А истинна,
В то выполняется и следствие В.
Примеры применения правила логического вывода.
1. «Если идет дождь, то на улице мокро».
«Пошел дождь».
Следовательно, «на улице мокро».
2. «Если кому-то весело, то он улыбается».
«Маша развеселилась».
Следовательно, «Маша улыбается».
В предикатной форме закон логического вывода превращается в процедуру вывода новых сведений из имеющихся общих правил и конкретных фактов:
А(х) ®
В(х), А(с) - Если из А(х) следует В(х) и А(х) выполнено
В(с) для х = с, то выполняется В (с).
Данная процедура из конкретного факта А(с)
и общего правила логического вывода А(х) ®
В(х) позволяет вывести новое
конкретное утверждение В(с).
Иными словами, эта процедура вывода позволяет выводить новые конкретные сведения из общих правил и уже известных конкретных фактов.
Следовательно, знание и применение законов логического вывода позволяет порождать новые сведения, являющиеся логическим следствием уже известных сведений.
Этим свойством и этими зако нами могут пользоваться не только люди - они применяются в системах машинного интеллекта.
Закон вывода отрицаний - второй закон логического вывода:
А ® В, не В - Если из А следует В, но следствие В ложно,
не А то не выполняется посылка А.
Примеры логического вывода из отрицаний.
1. «Если идет дождь, то на улице мокро».
«На улице сухо».
Следовательно, «На улице не было дождя».
2. «Если кому-то весело, то он улыбается».
«Вова не улыбается».
Следовательно, «Вове не весело».
В предикатной форме закон вывода отрицаний превращается в конструктивную процедуру вывода отрицаний:
А(х) ® В(х), не В(с)
- Если из А(х) следует
В(х), но В не выполнено
не А(с) для х = с, то не выполняется и А(с).
Данная процедура из конкретного отрицания следствия не В(с) и общего правила А(х) ®
В(х) выводит конкретное отрицание не А(с)
предпосылки при х = с. Эта процедура используется в системе Пролог как основной механизм поиска ответов на сложные вопросы, в которых участвуют определяемые предикаты.
В качестве иллюстраций дополним рассмотренную базу знаний о семье набором правил на языке Пролог, выражающих понятие «родитель»:
родитель (х, у) ¬ мама (х, у); - Мама - родитель
родитель (х, у) ¬ папа (х, у); - Папа – родитель
После ввода этих правил в ЭВМ система Пролог на вопросы о родителях выдаст такие ответы при указанной выше базе данных:
? родитель (Надя, х) - Кому родитель Надя ?
х = Оля
х = Сережа
Вывод ответов на эти вопросы система Пролог проводит следующим образом. Во-первых, вопрос ? родитель (Надя, х) будет заменен на отрицание не родитель (Надя,
х). Далее это отрицание будет сопоставлено с правилом вывода родитель (х, у) ¬ мама (х, у), а затем с правилом родитель (х, у) ¬ папа (х, у).
Применение этой же процедуры вывода ко второму определению родитель (х, у) ¬ папа (х, у) даст отрицание не папа (Надя, х), означающее утверждение «Надя не является папой никому». Для этого утверждения компьютер не имеет в базе данных никаких соответствующих фактов и после просмотра базы знаний по этому варианту выдает ответ НЕТ.
Применение к отрицанию не родитель (Надя, х) и определению родитель (х, у) ¬
мама (х, у) рассматриваемой процедуры приводит к выводу утверждения не мама (Надя, х), означающему «Надя не является мамой никому». Для этого отрицания машина найдет два конкретных противоречащих ему факта мама (Надя, Оля) и мама (Надя, Сережа). Используя конструктивную процедуру вывода ответов из отрицаний, компьютер даст два конкретных ответа - х = Оля и х = Сережа.
Закон тождества - четвертый общий логический закон, указанный Аристотелем:
«Предмет
рассмотрения должен быть определен
и не должен меняться до конца обсуждения»
Данный закон носит фундаментальный характер
для работы экспертных систем - правильные выводы и решения могут быть получены от экспертных систем только при строгом совпадении определений вещей из рассматриваемой предметной области.
Расхождения в понимании и определении предметных понятий могут приводить и, как правило, приводят к логическим ошибкам и получению неправильных выводов и результатов, что наблюдается среди людей, не обладающих необходимыми профессиональными знаниями.
Примером нарушения закона тождества является подмена предмета, когда два собеседника осознанно или неосознанно говорят о разных вещах, что приводит их к непониманию, спорам и разногласиям. Классический пример нарушения - ситуация: «я
- про Фому, а он - про Ерему».
В системе Пролог и в системах искусственного интеллекта вывод ответов на сложные вопросы основан на принципе унификации (взаимосогласования) ответов. По этой причине экспертные системы на ЭВМ в отличии от людей могут производить вывод ответов на сложные вопросы только в соответствии с принципом унификации.
Принцип унификации ответов состоит в том, что общие перемен ные во взаимосвязанных вопросах должны получать одинаковые значения. Пример ответа на сложносоставной вопрос, состоящий из двух подвопросов:
? мама (z, у), мама (у, Оля) - Кто мама у мамы Оли?
z = Зина
у = Надя
Вывод ответов на сложносоставные вопросы состоит в выделении подвопросов и поиске на них ответов по частям:
? мама (z, у), мама (у, Оля)
¤ \
? мама (z, у) ?мама
(у, Оля)
¤ \ ¤
z = Зина у = Надя
В данном примере общим элементом в выделяемых подвопросах ? мама (z, у) и ? мама (у, Оля) является переменная «у». Ответом на первый подвопрос ?
мама (z, у) будут значения z = Зина и у = Надя. Ответы на второй подвопрос ? мама (у, Оля) в соответствии с принципом взаимосогласования будет проводиться для значения у = Надя.
Принцип вывода взаимосогласованных ответов в системе Пролог распространяется и на сложносоставные правила, включаемые в базы знаний и процедуры логического вывода. Приведем примеры сложных определений:
бабушка (z, х) ¬ мама (z, у), мама (у, х);
бабушка (z, х) ¬ мама (z, у), папа (у, х);
дедушка (z, х) ¬ папа (z, у), мама (у, х);
дедушка (z, х) ¬ папа (z, у), папа (у, х);
При наличии этих правил в памяти ЭВМ можно получить следующие вопросы о бабушках и дедушках:
? бабушка (z, Оля) - Кто бабушка у Оли?
z = Зина
? дедушка (z, Надя) - Кто дедушка у Нади?
нет
Принцип унификации в системе и языке Пролог является общим механизмом логического вывода ответов на сложные вопросы в базах знаний на Прологе и тем самым - конструктивной реализацией закона тождества для машинных систем искусственного интеллекта. Таким образом работа экспертных систем на ЭВМ основана строго на выполнении требований законов логики
- закона тождества и закона достаточных оснований.
В о п р о с ы
1.
В чем состоит закон противоречия?
2. В чем заключается закон исключения третьего?
3. Как используется закон вывода следствий?
4. Как используется закон отрицания следствий?
5. В чем недостатки закона двойного отрицания?
6. В чем состоит закон достаточных оснований?
7. В чем заключается закон тождества?
8. В чем состоит принцип унификации?
9. Как согласуются ответы на сложные вопросы?
3 а д а н и я
1. Укажите примеры двойного отрицания для утверждений:
а) «сегодня был дождь»; в) «х = 2» и «х = 3»;
б) «х = 0» или
«у = 0»; г) «5 не делится на 2 и на 3».
2. Пусть утверждение А «прошел дождь», а утверждение В «на улице сыро». Истинны ли следующие суждения?
а) А Þ В (прямое доказательство);
б) В Þ А (обратное доказательство);
в) не А Þ не В (противоположное доказательство);
г) не В Þ не А (противоположное обратному).
3. Предложите систему признаков и понятий для описаний
а) класса «Млекопитающие»; в) класса «Рыбы»;
б) класса «Птицы»; г) класса «Насекомые».
В систему понятий введите следующие признаки: окрас, продолжительность жизни, умения ползать, летать, ходить и т. д.
4. Составьте базу знаний по всемирной географии. В базу знаний включите сведения о странах: название столицы, число жителей, тип государства, размеры страны, континент.
5. Составьте базу знаний по городам своей страны. В базу знаний включите сведения о размерах городов, числе жителей, расстоянии от столицы, названии самых крупных заводов, фабрик, музеев, стадионов и т. п.
6. Составьте базы данных
а) по литературе; г) по истории;
б) по зоологии; д) по ботанике;
в) об автомобилях; е) по кулинарии.