БЕЗ ВЗВЕШИВАНИЯ
В качестве второго примера приведем математическую задачу, решение которой, по мнению многих, невозможно без привлечения операций над числами с плавающей точкой. Мы покажем вам, как арифметика с фиксированной точкой позволяет решать довольно сложные уравнения, и при этом ни диапазон, ни точность представления чисел не ухудшаются.
Вычислим вес конусообразной «кучи» некоторого материала, зная ее высоту и угол откоса, а также плотность материала. Чтобы сделать нашу задачу более конкретной, давайте взвесим кучи песка, гравия и цемента. Крутизна каждой кучи, называется углом естественного откоса, зависит от вида материала. Например, песчаные кучи более крутые, чем из гравия.

(На самом деле эти величины колеблются в большом диапазоне в зависимости от разных факторов. Для иллюстрации мы выбрали приблизительные значения угла откоса и плотности.)
Существует формула вычисления массы конусообразной кучи высотой h (в футах), углом естественного откоса 9 (в градусах) и плотностью материала D (в фунтах на кубический фут)1:
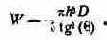
Запишем эту формулу на Форте. Условимся считать, что аргументы нашей программы будут вводиться в такой последовательности: название материала, например ПЕСОК, а затем высота кучи. В результате выполнения программы мы должны получить массу кучи сухого песка. Допустим, что для любого материала его плот-
1 Для скептиков. Объем конуса V вычисляется по формуле

где b - радиус основания; h - высота. Мы можем найти радиус основания, зная угол откоса, или, более точно, тангенс этого угла. Тангенсом некоторого угла называется отношение катета противолежащего (на рисунке h) к катету прилежащему (на рисунке b):
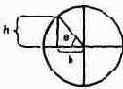
Если обозначить этот угол через


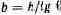
ность и угол естественного откоса остаются неизменными. Поэтому можно записать указанные две величины для каждого вида материала в некоторую таблицу.
Так как в конечном итоге нам потребуется тангенс угла, а не его величина в градусах, будем хранить значение тангенса. Например, угол естественного откоса для цемента составляет 35°, а его тангенс равен .700. Мы будем хранить это значение в виде целого 700.

Помните, что наша цель заключается не в том, чтобы просто получить результат. Мы составляем такую программу, по которой компьютер или иное вычислительное устройство выдает ответ самым быстрым, самым эффективным и самым точным способом. Как уже отмечалось в гл. 5, для записи математических выражений посредством арифметики с фиксированной точкой вам придется приложить немало усилий. Но вы будете вознаграждены за свои страдания. Во-первых, значительно увеличится скорость выполнения, что очень важно в тех случаях, когда какой-нибудь процесс разбивается на миллионы шагов или когда ежеминутно приходится производить несколько тысяч операций. Во-вторых, уменьшится размер программы и вы сможете, например, выполнить ее с помощью калькулятора, специально предназначенного для вычисления веса материала. Форт часто применяется в такого рода машинках.
Начнем решение задачи с установления порядка величин. Высота всех трех куч лежит в пределах от 5 до 50 футов. Вычислив массу кучи цемента, мы получим 35 000 000 фунтов. Но так как кучи не имеют форму правильного конуса, а мы берем средние зна чения величин, точность вычислений не может превышать четырех или пяти порядков1. Если перевести наш результат в тонны, то получим 17 500 т. Это значение вполне удовлетворяет представлению числа одинарной длины, так что в нашей программе условимся применять арифметические операции только над значениями одинарной длины.
Те программы, в которых требуется большая точность, могут быть написаны с использованием представления чисел двойной длины. Как вы увидите позднее, для сравнения мы даже создадим второй вариант нашей программы, где будут задействованы арифметические операции над 32-разрядными числами. Пока же мы хотим показать, что требуемую точность можно обеспечить, применяя операции Форта только с 16-разрядными значениями.
Выполнив вычисления для кучи высотой 40 футов, мы обнаружили, что изменение высоты на одну десятую может привести к изменению ее массы на 25 тонн. Поэтому входные данные будем исчислять не в целых футах, а в десятых долях фута. Желательно, чтобы пользователь имел возможность вводить следующее выражение: 15 ФУТОВ 2 ДЮЙМОВ КУЧА
где слова ФУТОВ и ДЮЙМОВ представляли бы футы и дюймы с точностью до десятых долей дюйма, а слово КУЧА производило бы необходимые вычисления. Слова ФУТОВ и ДЮЙМОВ можно было бы определить так:: ФУТОВ ( футы -- вес-в-масштабе) 10 * ; : ДЮЙМОВ { вес-в-масштайе -- вес-в-масштабе' ) 100 12 */ 5 + 10 / + ;
использование слова ДЮЙМОВ не обязательно. Таким образом, выражение 23 ФУТОВ поместит в вершину стека число 230, выражение 15 ФУТОВ 4 ДЮЙМОВ - число 153 и т. д. (Между прочим довольно легко организовать ввод данных и в десятых долях дюйма с десятичной точкой, например: 15.2. В таком случае слово NUMBER переводит вводимое число в значение двойной длины. Так как мы имеем дело только с числами одинарной длины, для того чтобы удалить старший байт, достаточно просто применить слово DROP.)
При написании определения КУЧА нужно попытаться обеспечить максимальную точность, не выходя за границы 15 разрядов. По нашей формуле первое, что требуется сделать, - возвести аргумент в куб. Однако напомним, что аргументом может служить
1 Для специалистов-математиков. На самом деле, так как высота в нашем примере выражается тремя цифрами, мы не можем ожидать точности большей, чем три порядка. Однако в учебных целях мы выберем точность, превышающую четыре порядка.
значение высоты вплоть до 50 футов, т. е. при выбранном масштабе 500. Даже если мы возведем это значение лишь в квадрат, то получим 250 000, что уже превышает возможности представления одинарной точности. Но для того чтобы выразить ответ в тоннах, рано или поздно в ходе вычислений нам придется выполнить деление на 2000, поэтому выражениеDUP DUP 2000 */
будет одновременно возводить аргумент в квадрат и переводить в тонны, так как под промежуточный результат в операции */ отводится слово двойной длины.
Если наш аргумент равен 500, то в результате получится 125.
Высота кучи может оказаться равной всего лишь пяти футам. Возведение этого значения в квадрат дает 25, а при делении последнего числа на 2000 средствами целочисленной арифметики мы получим нуль, что свидетельствует о неудачном выборе масштаба с небольшими значениями аргумента. Для обеспечения максимальной точности мы не должны при масштабировании получать меньшие значения, чем требуется. Число 250 000 вполне представимо средствами арифметики одинарных чисел, если его предварительно разделить на 10, поэтому мы начнем наше определение КУЧА следующим выражением:DUP DUP 10 */
На данном этапе результат с учетом масштабирования окажется в десять раз большим (25000 вместо 2500.0), чем требуется.
Далее необходимо возвести аргумент в куб. Непосредственное умножение опять приведет к результату двойной длины и, значит, масштабирование должно производиться с применением операции */. Как видите, выбрав в качестве делителя 1000, мы продолжаем оставаться в пределах одинарной длины. Теперь наш результат будет в десять раз меньшим (12 500 вместо 125 000), чем требуется, и все еще сохраняется точность в пять знаков. Согласно приведенной выше формуле нужно умножить аргумент на pi. Вы знаете, что на Форте это можно сделать с помощью следующего выражения: 355 113 */
Кроме того, мы должны разделить наш аргумент на три. Оба указанных действия можно осуществить посредством выражения 355 339 */
что не вызывает никаких проблем с масштабированием. Затем полученное выражение делим на квадрат тангенса (путем последовательного двойного деления на значение тангенса). Поскольку значение тангенса, хранимое в таблице, увеличено в 1000 раз, чтобы выполнить деление, нужно делимое умножить на 1000 и разделить на табличное значение тангенса:1000 ТЕТА @ */
Такое действие мы должны произвести дважды, поэтому оформим его в виде определения с именем /TAN (для деления-на-тангенс) и применим это определение дважды в определении слова КУЧА.
Наш результат пока еще будет в десять раз меньше, чем на самом деле (26711 вместо 267110 при максимальных значениях аргументов).
Нам остается лишь умножить полученное значение на величину плотности материала, максимальное значение которой равно 131 фунт на кубический фут. Во избежание переполнения уменьшаем плотность в 100 раз, применяя выражение ПЛОТНОСТЬ @ 100 */
Проверив выполнение программы в этой точке с данными о куче цемента высотой 50 футов, получим число 34991, что превышает 15 разрядов. Теперь пора принять во внимание значение 2000. Вместо ПЛОТНОСТЬ @ 100 */
мы можем написать: ПЛОТНОСТЬ @ 200 */
и наш ответ будет приведен к целому числу тонн.
Этот вариант программы вы найдете на распечатке блока 246, которая приводится ниже. Как уже упоминалось ранее, в блоке 248 находится вариант той же программы с использованием арифметических операций над данными двойной длины. Здесь вы вводите высоту в виде числа двойной точности с одним знаком после точки, представляющим десятые доли фута, например 50.0 футов, а далее следует слово ФУТЫ.
Выполняя целочисленные арифметические операции над числами двойной длины, мы в состоянии округлять полученный вес кучи до ближайшего целого фунта. В нашем случае применение целочисленной арифметики двойной длины открывает не меньшие
возможности, чем те, которые предоставляет более мощная арифметика с плавающей точкой. Ниже для сравнения приводятся результаты, полученные с помощью калькулятора, имеющего диапазон представления чисел в 10 десятичных цифр, средств Форта одинарной длины и средств Форта двойной длины. Результаты представлены для кучи цемента высотой 50 футов с использованием табличных значений: В ФУНТАХ В ТОННАХ --------------------------------------------- калькулятор 34.995.634 17,497.817 16-разрядный форт - 17.495 32-разрядный форт 34.995.634 17.497.817 ---------------------------------------------
Результаты же работы нашей программы таковы:246 LOAD ok ( компиляция варианта с одинарной длиной) ЦЕМЕНТ ok 10 ФУТОВ КУЧА = 138 тонн цемента ok 10 ФУТОВ 3 ДЮЙМОВ КУЧA = 1S1 тонн цемента ok СУХОЙ-ПЕСОК 10 ФУТОВ КУЧА = 81 тонн песка ok 248 LOAD ok ( компиляция варианта с двойной длиной) ЦЕМЕНТ ok 10.0 ФУТОВ = 279939 фунтов цемента или 139.969 тонн ok
Замечание по поводу компиляции строк. Определение слова МАТЕРИАЛ требует трех аргументов для каждого материала, одним из которых является адрес некоторой строки. Слово .МАТЕРИАЛ с помощью этого адреса выводит название рассматриваемого материала. Для помещения этой строки в словарь и передачи адреса слову МАТЕРИАЛ мы определили слово с именем ," (запятая-кавычки).
В первую очередь оно вносит в вершину стека значение HERE для слова МАТЕРИАЛ, так как именно по данному адресу будет компилироваться строка, а затем инициирует слово STRING для компиляции строкового литерала, ограниченного двойной кавычкой. В некоторых системах это слово можно определить следующим образом: : STRING ( с) WORD С@ 1 + ALLOT ;
Block # 246 0 \ Определение массы конической кучи - одинарная длина 1 VARIABLE ПЛОТНОСТЬ VARIABLE ТЕТА VARIABLE Н.М. 2 : ," ( --a) HERE ASCII " STRING ; 3 : .МАТЕРИАЛ Н.М. @ COUNT TYPE SPACE ; 4 : МАТЕРИАЛ ( 'строка плотность тета -- ) CREATE , , , 5 DOES> DUP @ ТЕТА ! 2+ DUP @ ПЛОТНОСТЬ ! 2+ @ Н.М. ! ; 6 7 : ФУТОВ ( футы -- вec-в-масштабе) 10 * ; 8 : ДЮЙМОВ ( вес-в-масштабе -- вес-в-масштабе') 9 100 12 */ 5 + 10 / + ; 10 11 : /TAN ( n - n') 1000 TETA @ */ ; 12 : КУЧА ( вес-в-масштабе -- ) 13 DUP DUP 10 */ 1000 */ 355 339 */ /TAN /TAN 14 ПЛОТНОСТЬ @ 200 */ ." = " . ." тонн " .МАТЕРИАЛ ; 15 247 LOAD
Block # 247 0 \ Таблица материалов 1 \ адрес-строки плотность тета 2 ," цемента" 131 700 МАТЕРИАЛ ЦЕМЕНТ 3 ," рыхлого гравия" 93 649 МАТЕРИАЛ РЫХЛЫЙ-ГРАВИЙ 4 ," плотного гравия" 100 700 МАТЕРИАЛ ПЛОТНЫЙ-ГРАВИЯ 5 ," сухого песка" 90 734 МАТЕРИАЛ СУХОЙ-ПЕСОК 6 ," мокрого песка" 118 900 МАТЕРИАЛ МОКРЫЙ-ПЕСОК 7 ," глины" 120 727 МАТЕРИАЛ ГЛИНА 8 9 10 11 12 ЦЕМЕНТ 13 14 15
Block # 248 0 \ Масса конической кучи - двойная длина 1 VARIABLE ПЛОТНОСТЬ VARIABLE TETA VARIABLE H.М. 2 : ," ( -- a) HERE ASCII " STRING ; 3 : .МАТЕРИАЛ Н.М. @ COUNT TYPE SPACE ; 4 : DU.3 ( du -- ) <# # # # ASCII .HOLD #S #> TYPE SPACE ; 5 : МАТЕРИАЛ ( 'строка плотность тета -- ) CREATE 6 DOES> DUP @ TETA ! 2+ DUP @ ПЛОТНОСТЬ ! 2+ @ Н.М. ! ; 7 : КУБ ( d -- d') 2DUP OVER 10 M*/ DROP 10 M*/ 8 : /TAN ( d -- d') 1000 TETA @ М*/ ; 9 : ФУТОВ ( d -- ) КУБ 355 339 M*/ ПЛОТНОСТЬ @ 1 М*/ 10 /TAN /TAN 5 M+ 1 I0 M*/ 11 2DUP ." = " D. ." фунтов " .МАТЕРИАЛ 12 1 2 M*/ ." или " DU.3 ." тонн " ; 13 247 LOAD 14 15
