Основы метрологии цвета

5.1. ПРИНЦИПЫ ИЗМЕРЕНИЯ ЦВЕТА

V

В основе любой точной науки лежат измерения, потому что раскрывая связи между явлениями, она прежде всего рассматривает количественные их соотношения. Экспери­ментальная проверка любого вывода требует проведения измерений. «Наука,— по словам Д. И. Менделеева,— начи­нается с тех пор, как начинают измерять». Английский фи­зик У. Томсон (Кельвин) сказал: «Каждая вещь известна лишь в той степени, в какой ее можно измерить».

Наука об измерениях называется метрологией. Техника — полиграфия, кинематография, репрография — производит репродукции цветных объектов. Работники про­мышленности имеют дело не только с технологией воспроиз­ведения, но и с методами определения качества продукции, а также материалов и промежуточных изображений — кра­сок, цветных негативов и т. д. Следовательно, практикам необходимо владеть методами цветовых измерений. Учение об измерении цвета называется метрологией ц в е -т а или колориметрией.

Колориметрия использует два способа количественного описания цветов. 1) Определение их цветовых координат и тем самым — строгих численных характеристик, по кото­рым их можно не только описать, но и воспроизвести. Сис­темы измерения Цвета называются колориметри­ческими (см.


главы 5—8). 2) Нахождение в некотором наборе эталонных цветов образца, тождественного данному. Совокупность образцов составляет систему, называемую системой спецификации (см. главу 10).

Для измерения цвета пользуются приборами, называе­мыми колориметрами. Колориметрическое определение ос­новано на том, что с помощью трех основных синтезируется цвет, тождественный измеряемому (рис. 5.1, а). Две грани белой призмы, наблюдаемые через окуляр, образуют фотометрическое поле, позволяющее сравнивать цветности и ин­тенсивности падающих на призму световых пучков. На од­ну половину поля направляют измеряемое излучение (ниж­няя грань призмы), на другую — основные. Их количества можно регулировать, например, с помощью диафрагм, се­ток или нейтральных оптических клиньев. Наблюдатель видит обе половины поля и изменяет соотношения количеств основных на той грани, где происходит синтез, так, чтобы уравнять цвета обеих половин поля. Зная характеристики



Рис. 5.1. Схемы,измерения цвета

светорегулирующих устройств, при которых достигается визуальное тождество полей, по значениям коэффициентов пропускания находят количества основных, нужных для синтеза цвета, тождественного измеряемому. Тем самым оп­ределяются координаты измеряемого цвета.

На рис. 5.1, б показана схема измерения цвета в том слу­чае, если он невоспроизводим по насыщенности. В этом случае, как было показано в разделе 4.3, одна или две ко­ординаты имеют отрицательные значения. Координаты цве­та характеризуют его исчерпывающим образом. Если они известны, цвет нетрудно воспроизвести.



5.2. КОЛОРИМЕТРИЧЕСКИЕ СИСТЕМЫ

Результаты любых измерений должны быть однозначны­ми и сопоставимыми. Это — одно из основных требований метрологии. Для его осуществления необходимо, чтобы ус­ловия измерения, от которых зависят их результаты, были постоянными, принятыми за норму. Совокупность нормиро­ванных условий измерения цвета составляет колориме­трическую систему. Нормируют цветности ос­новных, уровень яркости, единицы количеств основных, размеры фотометрического поля — все эти факторы опреде­ляют значения цветовых координат измеряемого цвета.



В основе любой колориметрической системы находятся цветности цветов триады, так как от них результаты измере­ний зависят в особенно большой степени. Это видно из кри­вых основных возбуждений (рис. 2.8). Например, реакция синечувствительных рецепторов на длину волны ? = 390 нм равна 0,02 единицы, а для ? = 410 нм — несколько более 0,20 единицы. Следовательно, излучения ? = 390 нм и Я = = 410 нм вызывают одинаковые реакции синечувствитель­ных рецепторов при мощностях, относящихся как 10:1. Это значит, что если за основной принят цвет монохромати­ческого ? = 390 нм, то синяя координата данного цвета в 10 раз больше, чем при основном ? = 410 нм. Естественно, что для любого другого цвета триады можно привести по­добный пример.

Основные излучения выбираются так, чтобы они в соот­ветствии с первым законом Грасмана были линейно незави­симыми. Этому требованию отвечают излучения синего, зе­леного и красного цветов. Тройка линейно независимых цветов называется триадой. Для измерения цвета мож­но воспользоваться разными триадами: основные могут за­нимать разные спектральные интервалы и участки спектра. Однако практически их число ограничено. Это связано с тем, что колориметрия предъявляет к основным не только требование линейной независимости, но и другие. Среди них — возможность легкого и точного осуществления основных и также возможно большая насыщенность воспро­изводимых триадой цветов.

Как известно из изложенного выше, с уровнем яр­кости объекта связана контрастная чувствительность глаза. Поэтому два участка разных цветов, различаемые при одной их яркости, могут оказаться неразличимыми при другой, когда чувствительность глаза понижается. Следовательно, условия колориметрических измерений целесообразно нор­мировать так, чтобы уровень яркости поля был оптималь­ным в отношении чувствительности глаза.

То же относится и к размерам фотометрического поля. Первоначально (1931 г.) его размер был установлен 2°, позднее (1964 г.) наряду с ним было принято более широкое поле — 10°.



Здесь мы рассмотрим две системы измерения цветов пока в общих чертах, чтобы использовать эти предварительные сведения в дальнейшем при более подробном изложении ко­лориметрии.

5.2.1. Система RGB

Предлагались разные триады основных. Их цвета долж­ны не только отвечать требованиям аддитивного синтеза, о котором упоминалось выше, но и требованиям метрологии, в частности хорошо воспроизводиться. Когда создавались колориметрические системы, лазер еще не был изобретен, и наиболее воспроизводимыми считались излучения газосвет­ных ламп, из которых с помощью светофильтра можно вы­делить монохроматические строго определенных длин волн. В 1931 г. на VIII сессии Международного комитета г вещению (МКО) за основные были приняты цвета следую­щих излучений:

красное ?R = 700 нм, легко выделяется с помощью «кру­того» красного светофильтра из спектра обычной лампы на­каливания;

зеленое ?G = 546,1 нм, линия е в спектре ртути; синее ?в = 435,8 нм, линия g в спектре ртути. Цвета этих излучений получили название цветов R, G, И а колориметрическая система, использующая их в качестве основных, — системы RGB.

Одновременно с этой системой была принятаофугая, ос­новные цвета которой выбраны сверхнасыщенными, -- XYZ. Система RGB в современной колориметрии практически не используется.Однако рассмотрим ее, так Kak основные этой системы легко представить, и это облегчаетупонимание общих принципов колориметрии. Освоив ее общие понятия и представления, будет легче понять причины введения не­реальных цветов XYZ, их преимуществалеред реальными, а также операции, производимые с ними. Принятая МКО система XYZ в известной степени основана на RGB: ние ее сверхнасыщенных цветов определялось относитель­но указанных реальных.

Количественные характеристики цветов триады RGB Для выражения количеств основных пользуются как энер­гетическими, так и световыми величинами. Однако для мет­пологий цвета обычные их меры не всегда удобны, и поэто­му наряду с обычными применяют специальные колориметрические единицы.



Можно экспериментально убедиться, что смесь основ ных, яркости которых (в кд-м-2) равны между собой, имеет не белый, а синий цвет. Из кривых основных возбуждений (рис. 2.8) видно, что равные мощности (в Вт) синего, крас-



Рис. 3.8. Пример эффекта Пуркине. Синий и красный квадраты имеют разную светлоту при разных освсщенностях



Рис. 4.1. Пространственное смешение цветов: желтого с пурпурным и пурпурного с голубым



Рис. 4.3. Образование цветов при наложении мазков желтой, пур­пурной и голубой красок



Рис. 13.5. К основному положению дубликационной теории.

Рядом с однокрасочными клиньями — простейшим ориги­налом-дубликатом показаны детали произвольного ориги­нала. Если не применять цветовой корректуры, то они бу­дут воспроизведены с теми же искажениями, что и соот­ветствующие им по цвету поля клиньевного и зеленого излучений также вызывают большую реак­цию синечувствительных рецепторов, чем остальных.

Удобно выбрать единицы измерения световых величин так, чтобы выраженные одинаковым их числом количества основных давали бы белую смесь (см. об этом в разделе

Опыт показывает, что если взять одну произвольную све­товую единицу красного излучения R, то для получения бе­лого цвета его нужно смешать с 4,59 таких же единиц зеле­ного G и 0,06 синего В.

Эти количества выбраны как относительные колоримет­рические световые единицы и называются яркости ы ми коэффициентами LR, LG и LB. Иногда их выра­жают в кд-м-2 и тогда называют абсолютными яр­костными коэффициентами.

Аналогичный подход к оценке качественно разных излу­чений рассматривался в разделе 2.3.1.

Для удобства перехода от световых к энергетическим ве­личинам яркости цветов R, G и В оценивают в так называе­мых яркостных единицах BR, BG и ВB:



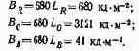
(5.1)

Если, например, отсчитаны две единицы BR, то это зна­чит, что яркость основного R составляет 2BR = 1360 кд-м-2 Руководствуясь тем же принципом, количества основных можно выражать в единицах световых потоков F:





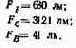
(5.1, а)

Единицы BR, ВG, BB и FR, FG, FB называются в об­щем случае световыми колориметричес­кими. Если ими пользуются при описании цвета, то цве­товым уравнениям придают вид



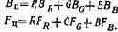
(5.2) (5.2,а)

Обычное же написание (4.1) означает, что основные вы­ражены в энергетических (мощностных) колориметрических единицах (см. ниже).

Яркости единичных цветов RGB (т. е. таких, модуль ко­торых т = 1) равны одной яркостной единице ВR, ВG или вb, так как яркость Вц любого единичного цвета в соот­ветствии с (5.2) равна



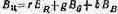
Приняв r = 1, получим g = b = 0. Следовательно, Вц

= = ВR = 680 кд-м-2, или Вц = BG = 3121 кд-м-2, если g = I.

Зная вид связи светового потока с потоком излучения, найдем по FR, FG и FB значения мощностей основных в Вт. Из физики известная формула, связывающая световой поток с потоком излучения:



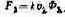
(5.3)

Учитывая, что мощности основных (т. е. потоки излуче­ния, переносимые ими) в колориметрии обозначаются буква­ми R, G и В, запишем:



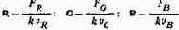
Заменяя F = 680L и взяв значения vr, vg и vb равными:



получим



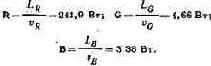
Эти единицы измерения величин R, G и В называются энергетическими (м о щ н о с т н ы м и) ко­лориметрическими.

Пользуясь формулой (5.3), можно установить соотноше­ния между световыми и энергетическими колориметричес­кими единицами:



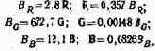
До сих пор говорилось о яр костных коэффициентах ос­новных цветов. Это понятие имеет более широкое значение. Яркостным коэффициентом цвета на­зывается его яркость, выраженная в колориметрических единицах при условии, что модуль цвета приведен к единице.

Установим связь между яркостью произвольного цвета и его яркостным коэффициентом. Так как яркость цвета рав­на сумме яркостей основных, его составляющих, то



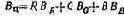
или, переходя от яркостей к яркостным коэффициентам,



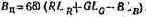
Вынося за скобки модуль, получим



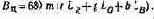
(5.4)

Произведение 680 т показывает, во сколько раз данный цвет отличается по яркости от единичного той же цветно­сти. Члены, стоящие в скобках, дают представление о доле, вносимой каждым из основных в яркость единичного цвета, поскольку r, g, b — его координаты.


Сумма этих долей рав­ на яркостному коэффициенту данного цвета Lц:



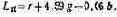
Заменяя в (5.4) сумму ее значением, получим



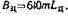
(5.5)

Из (5.5) следует, что яркостный коэффициент цвета пред­ставляет собой отношение



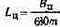
Так как Bц/т есть яркость Вед единичного цвета, то LЦ —

= 1/680 Вед и, следовательно, яркостный коэффициент любо­го цвета отвечает определению, которое дано выше.

5.2.2. Система XYZ

Одновременно с триадой RGB была принята другая трой­ка основных. Ее составили воображаемые цвета, более на­сыщенные, чем спектральные. Поскольку таких сверхнасы­щенных цветов в природе нет, их обозначили символами неизвестных величин X, Y и Z. Основанная на их примене­нии колориметрическая система получила название XYZ.

Одна из причин, побудивших ввести воображаемые сверх­насыщенные цвета, состоит в стремлении избавиться от от­рицательных цветовых координат, неизбежных в случае реальных цветов. А главное, система разработана так, что ряд колориметрических расчетов упрощается, и, в частнос­ти, это относится к выполняемым по формуле (5.5).

В этом разделе дано предварительное представление о си­стеме XYZ, а выбор основных, его обоснование изложены в разделе 7.3.

Пользоваться нереальными основными для непосредст­венного измерения цвета так, как это показано на рис. 5.2, невозможно. Принцип прямого определения координат X, Y, Z был реализован после изобретения фотоэлектрических ко­лориметров. А до этого их находили путем пересчета из не­посредственно измеренных координат R, G, В. Формулы пересчета даются в разделе 5.2.3.

Рабочей колориметрической системой, в которой выража­ются результаты измерения цвета, является XYZ, называ­емая международной, a RGB имеет значение вспомогатель­ной, иногда контрольной.

Основные цвета XYZ описываются в системе RGB следу­ющими уравнениями:



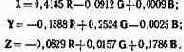
(5.6)

Их обоснование дается на с. 98.

Как видно из уравнений, цвет X близок по цветовому то­ну к R, хотя и заметно насыщеннее его (—0,0912 G).


Цвет Y много насыщеннее G: в цветовом уравнении две отрица­тельных координаты. Цвет Z несколько голубее В и более насыщен (—0,0829 R).

Воображаемые цвета X и Z не обладают яркостью. Яр- костные коэффициенты основных имеют значения: lx = 0, LY = 1, Lz = 0.

В таком случае (см. раздел 7.3) формула для расчета яр­кости приобретает вид

ВЦ = 680Y. (5.5,а)

Координаты XYZ можно находить по координатам непо­средственно измеряемых цветов RGB путем пересчета.

5.2.3. Переход от одной системы цветовых координат к другой

Пусть известно уравнение цвета Ц в некоторой системе основных, например RGB:

Ц=RR + GG + BB. (5.7)

 Требуется рассчитать координаты того же самого цвета, но в новой системе основных, например XYZ:



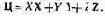
Для перехода к новым координатам (X, Y, Z) в общем случае необходимо измерить координаты старых основных RGB в новой системе XYZ.

Допустим, что измерения дали результаты:



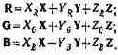
(5.8)

Заменим в уравнении (5.7) основные их значениями из (5.8) и, упростив, получим



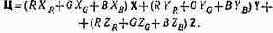
Откуда



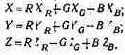
(5.9)

Следовательно, цветовые координаты некоторого цвета в новой системе равны сумме координат того же Цвета в ста­рой системе, причем каждая из них умножена на координа­ты старых основных, определенных в новой системе.

Результат расчета дает следующие формулы перехода:



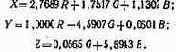
(5.10)

Уравнения (5.9) — формулы преобразования координат, известные из аналитической геометрии.

5.3. КРИВЫЕ СЛОЖЕНИЯ

Цветовые координаты можно определить не только изме­рением на колориметре (рис. 5.1), но и рассчитать их по кри­вым отражения образца (или пропускания, если он прозра­чен) и кривым сложения.

Кривыми сложения называются графики функций распределения по спектру цветовых координат мо­нохроматических излучений, имеющих мощность, равную



одному Вт. Такие координаты называются удельными, т. е. относящимися к единице мощности. Они обозначаются те­ми же буквами, что и координаты цветности, но с чертой на­верху. По стандарту (ГОСТ 13088—67) их выражают как функции длины волны, например r (?), g (?), b (?) или х (?), у (?), z (?).


В тех случаях, когда приводятся текущие значения удельных координат, их обозначают r?, g?, b? и аналогично в других системах.

Удельные координаты находят измерением цветов моно­хроматических излучений произвольной мощности и после­дующим делением их координат на мощность:



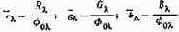
(5.11)

 Кривые сложения основных XYZ рассчитывают по фор­мулам (5.9) из экспериментально полученных r (?), g (?),

b (?). Значения удельных координат приводятся в колори­метрических справочниках (см. также табл. 6.1), а кривые сложения показаны на рис. 5.2.

Главная особенность кривых сложения хуг состоит в том, что одна из них — у? — совпадает по форме и положе­нию с кривой относительной световой эффективности (вид-ности). Площади, ограниченные каждой из кривых и осями координат, одинаковы между собой. Кривые, сложения, по­казанные на рис. 5.2, получены в результате тщательных исследований с применением совершенной измерительной техники при строгом соблюдении требований, предъявляе­мых колориметрией. Они включены в колориметрические и светотехнические справочники.

Кривые основных возбуждений (рис. 2.8) являются кри­выми сложения определенным образом выбранных основ­ных, так как характеризуют реакции цветочувствительных центров на постоянные по мощности (например, одноватт­ные) монохроматические излучения, а реакции эти могут служить цветовыми координатами некоторых нереальных цветов КЗС.

5.4. РАСЧЕТ ЦВЕТОВЫХ КООРДИНАТ

5.4.1. Связь цветовых координат с кривыми сложения

Если известны цветовые координаты монохромати­ческих излучений мощностью 1 Вт каждое, то расчетным пу­тем можно найти координаты цветов излучений произволь­ной мощности. Расчет основан на аддитивности цветовых координат. Из формул, связывающих цветовые координаты с удельными (5.11), следует, что для каждого из монохрома­тических излучений, входящих в данное сложное, можно записать:



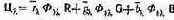
В соответствии с третьим законом Грасмана — законом аддитивности — цвет смеси излучений определяется суммой цветовых уравнений смешиваемых цветов, т.


е.



Откуда следует:



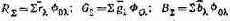
(5.12)

Если речь идет о цветах тел, не испускающих света, а от­ражающих его, то под знаки сумм нужно ввести значения монохроматических коэффициентов отражения поверхности, цвет которой оценивается. Если же определяется цвет про­зрачного тела, то вводится коэффициент пропускания. Это следует из отношений между упавшим на тело потоком и потоком, отраженным от него или поглощенным им:



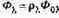
или



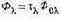
Тела природы имеют непрерывные кривые отражения или пропускания по всему спектру. Если функция распре­деления мощности источника по спектру также непрерывна, то цветовые координаты цвета отражающей поверхности можно выразить в интегральной форме:



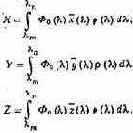
(5.13)

Для расчета цвета светопропускающей среды пользуют­ся аналогичными формулами, но функции отражения заме­няют функциями спектрального пропускания.

Формулы (5.13) справедливы не только для системы XYZ, в обозначениях которой они даны, но и для любой системы основных.

5.4.2. Колориметрические источники света

В формулы (5.13) входит функция Ф0 (?). Поэтому цвета несветящихся тел можно описать, лишь приняв во внимание спектральный состав падающего на них света. Между тем существует не только множество излучателей, но каждый из них может иметь разные распределения потока по длинам волн. Например, состав солнечного света зависит от време­ни дня, времени года, облачности неба и других факторов. Спектр лампы связан с режимами ее питания. Чтобы избежать большого количества близких характеристик цвета одного и того же образца, число возможных- излучателей, применя­емых при, цветовых измерениях, регламентируют. Цвет об­разца относят только к стандартному источнику. ГОСТ 7721 —76 устанавливает четыре колориметрических источни­ка. Они обозначаются буквами А, В, С и D65.

Источник А — норма среднего искусственного света. Он имеет то же распределение даваемого им потока излучения в видимой части спектра, что и абсолютно черное тело при тем­пературе 2856 К. Это — средняя цветовая температура ламп накаливания.


Источник представляет собой калиброванную лампу (т. е. имеющую определенный спектр испускания при данных режимах питания). Координаты цветности А: х = = 0,443; у = 0,407.

Источник В — норма прямого солнечного света. Стан­дарт регламентирует не цветовую температуру колоримет­рических источников В, С и D65, а распределения плотно­сти потока излучения в их спектрах. Для источника В оно соответствует цветовой температуре, близкой к 4800 К. Что­бы его воспроизвести, калиброванную лампу экранируют светофильтром. Координаты цветности излучения В (0,348; 0,352).

Источник С — норма рассеянного дневного света. Он представляет собой также калиброванную лампу со свето­фильтром. Цветовая температура превышает 6500 К. Коор­динаты цветности С (0,310; 0,316).

Источник D65 имеет цветовую температуру, почти стро­го равную 6500 К. Координаты D65 (0,313; 0,329). Реко­мендуется при измерении цвета люминесцирующих образцов. Поэтому распределение потока излучения в ультрафиоле­товой части его спектра, в отличие от источника С, норми­ровано.

Кроме стандартных источников в колориметрии рассмат­ривается еще так называемый равноэнергетический, для обозначения которого пользуются буквой Е. На любой его спектральный интервал данной ширины приходится одна и та же энергия Это значит, что его спектральная характе­ристика — прямая, параллельная оси длин волн.

В колориметрических справочниках приводятся коорди­наты цветности, а также так называемые кривые сложения при данных источниках, представляющие собой произведе­ние удельных координат на монохроматические мощности.

5.4.3. Примеры расчета

Яркости несветящихся тел зависят от их освещенности-Поэтому для описания цветов таких тел целесообразно поль­зоваться не абсолютными, а относительными цветовыми ко ординатами.

По относительным значениям цветовых координат, полу­ченным на основании указанного расчета, можно определить координаты цветности. Для этого, как обычно, цветовые ко­ординаты (в данном случае относительные координаты) нужно разделить на модуль.


Переход же от координат цветности к абсолютным значениям цветовых координат цвета данного излучения не вызывает затруднений, если известна яркость В или мощность Ф.

Пусть, например, яркость излучения В = 340 кд-м~2, х = 0,5, у = 0,4. Для 'перехода к цвету требуется найти ко­ординату, которая несет сведения о яркости излучения.

Так как В = 680 Y, то Y = 340:680 = 0,5. Следова­тельно, и остальные цветовые координаты в 0,5:0,4 =1,25 раза больше координат цветности. Если учесть, что исход­ное значение Z = 0,1, то уравнение цвета излучения име­ет вид



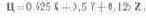
Цветовые координаты несветящихся объектов рассчиты­ваются по формулам (5.13), в которых Ф0 (?) заменяется од­ной из нормированных, как это было показано выше, функ­ций ФA0(?), ФB0(?), ФC0(?) или ФD0?, — относительного распре­деления энергии в спектре колориметрического источника. Ординаты кривых сложения, кривых распределения энер­гии в спектре источника и кривых пропускания образца (или его отражения, если рассчитывается цвет поверхности непрозрачного образца) перемножают. Их берут через спект­ральные интервалы 5—20 нм в зависимости от требований к точности определений. В результате получают кривые X (?), Y (?.), Z(?). Ограниченные ими площади пропорцио­нальны значениям цветовых координат.

Это показано на рис. 5.3 на примере вычисления ордина­ты Х? (т. е. взятой при длине волны ?) кривой X (?) зеленого светофильтра -- пластинки из стекла ЗСЗ (ГОСТ 9411—66) —при источ­нике В. Функции, выражае­мые кривыми а и б, даются в колориметрических справоч­никах. При расчете цвета от­ражающей поверхности функ­цию ? (?) заменяют на ? (?).

Таким образом, расчет по общему методу состоит в чис­ленном интегрировании выра­жений (5.13), т. е. нахождении площадей под кривыми X (?), Y (?) и Z (?). Напомним, что численное интегрирование по формулам прямоугольников заключается в суммировании произведений типа Ф0?

х?р ??, т. е. площадей прямоуголь­ников, высота которых -среднее значение Ф0?


Содержание раздела

---

---