Равноконтрастные колориметрические системы
8.1. ПОРОГОВЫЕ ЭЛЛИПСЫ НА ГРАФИКЕ хуГрафики rg и ху дают достаточно полные сведения о свойствах цветов. Зная положение точки на графике, нетрудно указать координаты цветности выражаемого ею цвета, определить яркость единичного цвета, доминирующую длину волны и колориметрическую чистоту. Легко найти сумму нескольких цветов и характеристики суммарного цвета. Однако указанные графики не дают точной информации о степени зрительного различия цветов, особенно контрастирующих по цветовому тону.
Знакомясь с закономерностями зрительного восприятия (раздел 3.2), мы пользовались понятием о порогах, установив в качестве меры цветовых различий пороги восприятия яркости, насыщенности и цветового тона.
Исследователями была поставлена задача определения степени различаемости цветов в зависимости от их положения на диаграмме ху. Сложность задачи — в необходимости сравнивать цвета, которые неодинаковы сразу по нескольким параметрам.
В опытах, например по измерению порогов цветового тона, изменялась только одна характеристика — длина волны (см. с. 35). В подобных условиях определяли и другие пороги. На поле же цветовой диаграммы яркость, цветовой тон и насыщенность изменяются одновременно. Яркость падает по вертикали, насыщенность уменьшается по мере приближения к белой точке, цветовой тон изменяется по локусу. Пороги различения, определенные при изменении всех трех характеристик, называются цветовыми или порогами цветоразл и ч е н и я.
Впервые они были определены Джаддом, который нашел их расположение на диаграмме ху. Он показал, что точки цветов А, В, С, D, Е, F, G, H, J (рис. 8.1), минимально отличимых от данного Ц, расположены по эллипсу. Точка данного цвета (т. е. исходная) находится в пересечении его осей. Указанные эллипсы были названы пороговыми. Их размеры, соотношения осей и их направление зависят от положения исходной точки Ц на графике. Пороги определялись исходя из среднеквадра-тической ошибки при установлении колориметрического тождества. По М. М. Гуревйчу, порог цветоразличения приблизительно в три раза больше ошибки.
Мак-Адам, проведя тщательные исследования, уточнил размеры и положение пороговых эллипсов. Его данные легли в
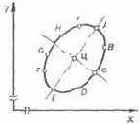
Рис. 8.1. Схема порогового эллипса

Рис. 8.2. Пороговые эллипсы на графике ху по
Мак-Адаму основу современных представлений о порогах цветоразличения. На рис. 8.2 показана полученная им диаграмма. Размеры эллипсов для наглядности увеличены им в десять раз.
Из рисунка видно, что пороги цветоразличения неравномерно распределены по графику. В его нижней, «сине-фиолетовой», части две близко расположенные точки выражают цвета, сравнительно сильно различающиеся зрительно. Чувствительность глаза.к изменению цветности здесь, велика. А в верхней, «зеленой», области даже минимальна ощутимое изменение цветности выражается довольно далеко отстоящими друг от друга точками.
Цветовой порог зависит не только от положения опорной точки на графике, но и от направления, по которому изменяется цветность.. Например, в верхней части графика порог сильно возрастает с изменением координаты у, а в нижней — координаты х.
Число порогов цветоразличения между двумя цветами называется цветовым контрастом.
Из сказанного понятно, что расстояние между точками двух цветов на графике ху непропорционально цветовому контрасту между ними. Если, например, разность координат цветов Ц1 и Ц2
такая же, как и разность координат другой пары цветов — Ц1 и Ц2, то нельзя сказать, что цветовой контраст между цветами указанных пар одинаков.
8.2. РАВНОКОНТРАСТНАЯ СИСТЕМА МКО-60
Для того чтобы обойти неудобства, связанные с нерав-ноконтрастностью системы XYZ, существуют два пути. Один из них состоит в создании формул пересчета, позволяющих переходить от характеристик, определяющих положение цветов на графике, к характеристикам, дающим представление о цветовом контрасте между ними. Наряду с этим целесообразно превратить цветовую диаграмму ху в такую, которая давала бы наглядное представление не только о координатах цветов, но и о цветовом контрасте между ними. Для этого нужно найти преобразование, которое позволило бы:
1) превратить пороговые эллипсы в окружности;
2) придать им одинаковые размеры;
3) не нарушать основных метрических свойств диаграммы. При этом оно должно быть достаточно простым, проективным.
Аффинное проецирование (рис. 6.15) не позволяет удовлетворить второе требование. Так как эллипсы нерав-ноконтрастной диаграммы имеют разные размеры, то сжимать их или растягивать нужно по-разному, а сделать это аффинное преобразование не позволяет.
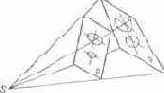
Рис. 8.3. Схема центрально-аффинного преобразования
Превращение диаграммы ху в равноконтрастную достигается путем центрально-аффинного проецирования. Рассмотрим его принципы. На рис. 8.3 показаны прямоугольник и два эллипса, лежащие в плоскости Р, и результат их центрального проецирования из точки S в плоскость Р', находящуюся под некоторым углом к Р. При таком проецировании, называемом центрально-аффинным, вертикальные оси эллипсов на проекции удлиняются, а соотношение размеров фигур на проекции получается иным, чем в оригинале.
Формулы проективной гео метрии позволяют найти угол между плоскостями Р к Р' и положение точки S, при которых эллипсы на проекции изображаются как окружности, имеющие одинаковый диаметр.
Подобный принцип используется для превращения диаграммы ху в приблизительно равноконтрастную. Так как направления больших осей эллипсов на диаграмме, показанной на рис. 8.2, различны, то в результате центрально-аффинного проецирования пороговые эллипсы превращаются в фигуры, лишь близкие к окружностям одинакового диаметра. Поэтому идеальное решение задач, поставленных выше, на основе описанного здесь метода преобразования невозможно. Было доказано, что для получения идеальных окружностей одного размера исходную диаграмму необходимо проецировать не на плоскость, а на искривленную поверхность. Тем не менее, проецируя на плоскость, можно существенно приблизиться к равноконтрастности диаграммы: если на исходной диаграмме оси эллипсов могут различаться в 20 раз, то на проекционно преобразованной их отношение в худшем случае составляет 2:1.
Результат проекционного преобразования диаграммы ху с целью превращения пороговых эллипсов Мак-Адама в окружности показан на рис. 8.4. Как видно, искажаются не только эллипсы, но и другие элементы графика — ло-кус, координатная сетка, которая в соответствии с рис. 8.3 сжимается в верхней части и расширяется в нижней. Естественно, что пользоваться сеткой с непрерывно изменяющимся масштабом неудобно. Поэтому выбрана новая система координат, в которой масштаб не зависит от положения точки. Ось абсцисс обозначается буквой и, ось ординат — буквой v.
Проекционно преобразованный график Мак-Адама положен в основу равноконтрастной колориметрической системы, называемой по основным цветам системой UVW. Она была принята МКО в 1960 г. и поэтому часто называется системой МКО-60. Ее основные цвета, как и XYZ, нереальны.
Расчет по соотношениям проективной геометрии дает следующий переход от координат xyz к координатам uvw:

(8.1)
И наоборот,
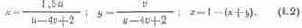
На цветовой диаграмме, приведенной на рис. 8.4, показана точка А, координаты которой х = 0,4, у = 0,2 или и = 0,35, v = 0,26. Указанное соотношение между координатами ху и uv, найденное графически, следует и из формул (8.1) и (8.2).
Для определения координат и, v no координатам XYZ применяются формулы:
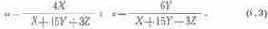
Поскольку система МКО-60 равноконтрастна, то расстояние между любыми двумя точками цветности на графике и, v выражает цветовой контраст, мера которого — число порогов цветоразличения. На рис. 8.4 показаны точки Ц1 и Ц2. Расстояние между ними ?E равно
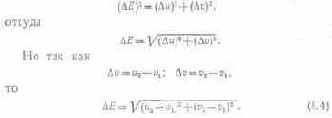
Зная координаты цветности двух цветов на графике ху, нетрудно рассчитать число порогов между ними. Для этого по формулам, связывающим координаты х, у и и, v, находят координаты сравниваемых цветов в равноконтрастной системе, а затем вычисляют ?E. Вследствие неточного

Рис. 8.4. Преобразование графика ху в равноконтрастный график иv
превращения эллипсов в окружности формула (8.4) носит приближенный характер.
Система МКО-60 разработана с довольно ограниченной целью получения равноконтрастной цветовой диаграммы.
8.3. РАВНОКОНТРАСТНАЯ СИСТЕМА МКО-64
В 1964 г. МКО по предложению Вышецки рекомендовал равноконтрастную систему U* V* W*, называемую также МКО-64. Ее главная особенность по сравнению с системой МКО-60 состоит во введении равноконтрастного цветового пространства.
Система опирается на следующие соотношения, найденные эмпирически:

(8.5)
где
W* - показатель светлоты; Y -- координата в системе XYZ, т, е. характеристика яркости.
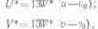
где U* и V* — показатели хроматичности; u и v — координаты цветности в системе МКО-60, определяемые по формулам (8.3); и0 и v0 — координаты белого цвета.
Цветовой контраст определяется по формуле МКО64-
(8.6)
Измерение цветового контраста необходимо при определениях допусков на цвета (красочная, текстильная промышленность), на цветовоспроизведение (кинопромышленность, полиграфия). Кроме формул (8.4) и (8.6) было предложено множество других, что свидетельствует об отсутствии единого мнения о расчете цветовых различий.
